Partie 3
Les Tests

Préambule : le Codage

Introduction à l'algorithmique

1. Les Variables

2. Lecture et Ecriture

3. Les Tests
     De quoi s'agit-il ?
     Structure d'un test
     Qu'est-ce qu'une condition ?
     Conditions composées
     Test imbriqués
     De l'aiguillage à la gare de tri
     Variables booléennes

4. Encore de la Logique

5. Les Boucles

6. Les Tableaux

7. Techniques Rusées

8. Tableaux Multidimensionnels

9. Fonctions Prédéfinies

10. Fichiers

11. Procédures et Fonctions

12. Notions Complémentaires

Liens

Souvent Posées Questions

« C’est assez difficile de trouver une erreur dans son code quand on la cherche. C’est encore bien plus dur quand on est convaincu que le code est juste. »
Steve McConnell

« Il n’existe pas, et il n’existera jamais, de langage dans lequel il soit un tant soit peu difficile d’écrire de mauvais programmes ».
Anonyme

« Si le déboguage est l’art d’enlever les bogues, alors la programmation doit être l’art de les créer. »
Anonyme

Je vous avais dit que l’algorithmique, c’est la combinaison de quatre structures élémentaires. Nous en avons déjà vu deux, voici la troisième. Autrement dit, on a quasiment fini le programme.

Mais non, je rigole.

1. De quoi s’agit-il ?

Reprenons le cas de notre « programmation algorithmique du touriste égaré ». Normalement, l’algorithme ressemblera à quelque chose comme : « Allez tout droit jusqu’au prochain carrefour, puis prenez à droite et ensuite la deuxième à gauche, et vous y êtes ».

Mais en cas de doute légitime de votre part, cela pourrait devenir : « Allez tout droit jusqu’au prochain carrefour et là regardez à droite. Si la rue est autorisée à la circulation, alors prenez la et ensuite c’est la deuxième à gauche. Mais si en revanche elle est en sens interdit, alors continuez jusqu’à la prochaine à droite, prenez celle-là, et ensuite la première à droite ».

Ce deuxième algorithme a ceci de supérieur au premier qu’il prévoit, en fonction d’une situation pouvant se présenter de deux façons différentes, deux façons différentes d’agir. Cela suppose que l’interlocuteur (le touriste) sache analyser la condition que nous avons fixée à son comportement (« la rue est-elle en sens interdit ? ») pour effectuer la série d’actions correspondante.

Eh bien, croyez le ou non, mais les ordinateurs possèdent cette aptitude, sans laquelle d’ailleurs nous aurions bien du mal à les programmer. Nous allons donc pouvoir parler à notre ordinateur comme à notre touriste, et lui donner des séries d’instructions à effectuer selon que la situation se présente d’une manière ou d’une autre. Cette structure logique répond au doux nom de test. Toutefois, ceux qui tiennent absolument à briller en société parleront également de structure alternative.
 

Retour Haut de Page
 

2. Structure d’un test

Il n’y a que deux formes possibles pour un test ; la forme de gauche est la forme complète, celle de droite la forme simple.

Ceci appelle quelques explications.

Un booléen est une expression dont la valeur est VRAI ou FAUX. Cela peut donc être (il n’y a que deux possibilités) :

·         une variable de type booléen

·         une condition

Nous reviendrons dans quelques instants sur ce qu’est une condition en informatique.

Toujours est-il que la structure d’un test est relativement claire. Arrivé à la première ligne (Si…Alors) la machine examine la valeur du booléen. Si ce booléen a pour valeur VRAI, elle exécute la série d’instructions 1. Cette série d’instructions peut être très brève comme très longue, cela n’a aucune importance. A la fin de cette série d’instructions, au moment où elle arrive au mot « Sinon », la machine saute directement à la première instruction située après le « Finsi ». De même, au cas où le booléen a comme valeur « Faux », la machine saute directement à la première ligne située après le « Sinon » et exécute l’ensemble des « instructions 2 ».

La forme simplifiée correspond au cas où l’une des deux « branches » du Si est vide. Dès lors, plutôt qu’écrire « sinon ne rien faire du tout », il est plus simple de ne rien écrire.

Exprimé sous forme de pseudo-code, la programmation de notre touriste de tout à l’heure donnerait donc quelque chose du genre :
 

Retour Haut de Page
 

3. Qu’est ce qu’une condition ?

Cette définition est essentielle ! Elle signifie qu’une condition est composée de trois éléments :

·         une valeur

·         un opérateur de comparaison

·         une autre valeur

Les valeurs peuvent être a priori de n’importe quel type (numériques, caractères…). Mais si l’on veut que la comparaison ait un sens, il faut que les deux valeurs de la comparaison soient du même type !

Les opérateurs de comparaison sont :  

·         =    égal à…

·         <> différent de… 

·         <    strictement plus petit que…  

·         >    strictement plus grand que…  

·         =< plus petit ou égal à…  

·         >= plus grand ou égal à…

L’ensemble des trois éléments constituant la condition constitue donc, si l’on veut, une affirmation, qui a un moment donné est VRAIE ou FAUSSE.

A noter que ces opérateurs de comparaison peuvent tout à fait s’employer avec des caractères. Ceux-ci sont codés par la machine dans l’ordre alphabétique (rappelez vous le code ASCII vu dans le préambule), les majuscules étant systématiquement placées avant les minuscules. Ainsi on a :
 

Retour Haut de Page
 

4. Conditions composées

Certains problèmes exigent parfois de formuler des conditions qui ne peuvent pas être exprimées sous la forme simple exposée ci-dessus. Reprenons le cas « Toto est inclus entre 5 et 8 ». En fait cette phrase cache non une, mais deux conditions. Car elle revient à dire que « Toto est supérieur à 5 et Toto est inférieur à 8 ». Il y a donc bien là deux conditions, reliées par ce qu’on appelle un opérateur logique, le mot ET.

Comme on l’a évoqué plus haut, l’informatique met à notre disposition quatre opérateurs logiques : ET, OU, NON, et XOR.

·     Le ET a le même sens en informatique que dans le langage courant. Pour que :

Condition1 ET Condition2

soit VRAI, il faut impérativement que Condition1 soit VRAI et que Condition2 soit VRAI.

·     Il faut se méfier un peu plus du OU. Pour que :

Condition1 OU Condition2

soit VRAI, il suffit que Condition1 soit VRAIE ou que Condition2 soit VRAIE. Le point important est  que si Condition1 est VRAIE et que Condition2 est VRAIE aussi, Condition1 OU Condition2 est VRAIE. Le OU informatique ne veut donc pas dire « ou bien » (sauf dans certaines formes rares, dénommées OU exclusif et notées XOR).

·     Le XOR (ou OU exclusif) fonctionne de la manière suivante. Pour que

Condition1 XOR Condition2

soit VRAI, il faut que Condition1 soit VRAI, ou bien que Condition2 soit VRAI. Mais si toutes les deux sont fausses, ou que toutes les deux sont VRAI, alors le résultat global est considéré comme FAUX.

J’insiste sur le fait que le XOR est une rareté, dont il n’est pas strictement indispensable de s’encombrer en programmation.

·     Enfin, le NON inverse une condition :

NON(Condition1)

est VRAI si Condition1 est FAUX, et il sera FAUX si Condition1 est VRAI.

Vous vous demandez peut-être à quoi sert ce NON. Après tout, plutôt qu’écrire NON(Prix > 20), il serait plus simple d’écrire tout bonnement Prix=<20.  Dans ce cas, c’est évident qu’on se complique inutilement la vie avec le NON. Mais on rencontrera plus loin des situations dans lesquelles il rend de précieux services.

On représente fréquemment tout ceci dans des tables de vérité (C1 et C2 représentent deux conditions, et on envisage à chaque fois les quatre cas possibles) : 
 

Retour Haut de Page
 

5. Tests imbriqués

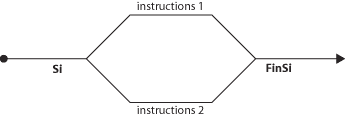
Graphiquement, on peut très facilement représenter un SI comme un aiguillage de chemin de fer (ou un aiguillage de train électrique, c’est moins lourd à porter). Un SI ouvre donc deux voies, correspondant à deux traitements différents. Mais il y a des tas de situations où deux voies ne suffisent pas. Par exemple, un programme devant donner l’état de l’eau selon sa température doit pouvoir choisir entre trois réponses possibles (solide, liquide ou gazeuse).

Une première solution serait la suivante :
 

Vous constaterez que c’est un peu laborieux. Les conditions se ressemblent plus ou moins, et surtout on oblige la machine à examiner trois tests successifs alors que tous portent sur une même chose, la température (la valeur de la variable Temp). Il serait ainsi bien plus rationnel d’imbriquer les tests de cette manière :

 Nous avons fait des économies : au lieu de devoir taper trois conditions, dont une composée, nous n’avons plus que deux conditions simples. Mais aussi, et surtout, nous avons fait des économies sur le temps d’exécution de l’ordinateur. Si la température est inférieure à zéro, celui-ci écrit dorénavant « C’est de la glace » et passe directement à la fin, sans être ralenti par l’examen d’autres possibilités (qui sont forcément fausses).

Cette deuxième version n’est donc pas seulement plus simple à écrire et plus lisible, elle est également plus performante à l’exécution.

Les structures de tests imbriqués sont donc un outil indispensable à la simplification et à l’optimisation des algorithmes. 
 

Retour Haut de Page
 

6. De l’aiguillage à la gare de tri

« J'ai l'âme ferroviaire : je regarde passer les vaches » (Léo Ferré)

Cette citation n’apporte peut-être pas grand chose à cet exposé, mais je l’aime bien, alors c’était le moment ou jamais.

En effet, dans un programme, une structure SI peut être facilement comparée à un aiguillage de train. La voie principale se sépare en deux, le train devant rouler ou sur l’une, ou sur l’autre, et les deux voies se rejoignant tôt ou tard pour ne plus en former qu’une seule, lors du FinSi. On peut schématiser cela ainsi :

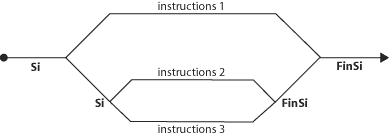
Mais dans certains cas, ce ne sont pas deux voies qu’il nous faut, mais trois, ou même plus. Dans le cas de l’état de l’eau, il nous faut trois voies pour notre « train », puisque l’eau peut être solide, liquide ou gazeuse. Alors, nous n’avons pas eu le choix : pour deux voies, il nous fallait un aiguillage, pour trois voies il nous en faut deux, imbriqués l’un dans l’autre.

Cette structure (telle que nous l’avons programmée à la page précédente) devrait être schématisée comme suit :

 Soyons bien clairs : cette structure est la seule possible du point de vue logique (même si on peut toujours mettre le bas en haut et le haut en bas). Mais du point de vue de l’écriture, le pseudo-code algorithmique admet une simplification supplémentaire. Ainsi, il est possible (mais non obligatoire, que l’algorithme initial :
 

devienne :

Le SinonSi permet en quelque sorte de créer (en réalité, de simuler) des aiguillages à plus de deux branches. On peut ainsi enchaîner les SinonSi les uns derrière les autres pour simuler un aiguillage à autant de branches que l’on souhaite.
 

Retour Haut de Page
 

7. Variables Booléennes

Jusqu’ici, nous avons utilisé uniquement des conditions pour faire des tests. Mais vous vous rappelez qu’il existe un type de variables (les booléennes) susceptibles de stocker les valeurs VRAI ou FAUX. En fait, on peut donc entrer des conditions dans ces variables, et tester ensuite la valeur de ces variables.

Reprenons l’exemple de l’eau. On peut le réécrire ainsi :
 

A priori, cette technique ne présente guère d’intérêt : on a alourdi plutôt qu’allégé l’algorithme de départ, en ayant recours à deux variables supplémentaires. Mais :

·         souvenons-nous : une variable booléenne n’a besoin que d’un seul bit pour être stockée. De ce point de vue, l’alourdissement n’est donc pas considérable.

·         dans certains cas, notamment celui de conditions composées très lourdes (avec plein de ET et de OU tout partout) cette technique peut faciliter le travail du programmeur, en améliorant nettement la lisibilité de l’algorithme. Les variables booléennes peuvent également s’avérer très utiles pour servir de flag, technique dont on reparlera plus loin (rassurez-vous, rien à voir avec le flagrant délit des policiers).

Retour Haut de Page